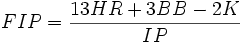In previous installments of this series we’ve covered the basic offensive, defensive, and pitching stats we use when discussing player production. Those familiar with the statistics will recognize what it means when we say a player has a .355 wOBA. Those who aren’t, though, might have a bit of trouble determining exactly what that means, even if they’re familiar with the workings of the statistic. To make things easier, we have a number of stats which compare production to the league average. We’ll dive into these today.
OPS+
Baseball Reference has changed the way we view statistics. The site makes everything presentable and easy to access, so we can look up our favorite players and see exactly what they did. One statistic that B-R founder Sean Forman created was OPS+. OPS, as you likely already know, stands for On-Base Plus Slugging. Since the ability to get on base and the ability to hit for power represent two of the most important things a batter can do, mashing the two stats together made enough sense, even if it double-counts singles — not to mention combines two stats that have different denominators.
The other problem with OPS is that it deals with two statistics on different scales. The maximum OBP is 1.000, while the maximum SLG is 4.000. The answer, then, is to weight the statistics when combining. Forman went with (1.2*OPB) + SLG, and then placed that figure on a scale where 100 was league average. That made the stat easier to understand. Instead of having just a number, OPS+ put the number in context by comparing it to everyone else in the league. Now we know that when a player has a 120 OPS+ that he’s well above league average. We might not have been able to discern that by just seeing a, for example, .870 OPS by itself.
Improved as it may be, OPS+ is not perfect. For instance, Tom Tango believes that OPS+ still undervalues OBP, and that the calculation should be (1.8*OBP) + SLG. Even so, OPS+ is an improvement over straight OPS, not just because of the 1.2*OBP calculation, but also because of how easily it tells us what we want to know. But, perhaps there’s a better stat for this.
wRC+
Uh oh. Another stat with a lower-case letter. For some this might mean trouble. It’s not, though. In fact, it works right along with wOBA to provide us with a scaled view of player production.
The story of wRC+ doesn’t go back too far. In December Alex Remington wrote a wOBA primer, and Tango made a comment about one of Alex’s lines regarding wOBA in relation to OPS and OPS+. Later, in the comments, Tango said that he did not want wOBA+, but rather wRC+ — weighted Runs Created on a league scale. He used the BaseRuns formula to demonstrate how easy it would be to implement, and FanGraphs proprietor David Appelman (a great guy, really!) implemented it. The whole process took about a day. No joke.
The basics of wRC+ can be found in the wOBA primer. It uses the same system, basically, but instead of outputting a rate stat it outputs a counting stat, weighted Runs Created, or wRC. The number is park adjusted and scaled to the league. Like OPS+, 100 is league average. I prefer wRC+ to OPS+ not only because of the slight flaw in the OPS+ calculation, but because it assigns a proper value to each component, whereas OPS+ still uses the arbitrary measures of two for a double, three for a triple, etc.
ERA+
Like OPS+, ERA+ can be found at Baseball-Reference. This one won’t take but a paragraph to explain. Like OPS+, ERA+ is on a scale where 100 is league average. You can compute it right from home, too. Just take two minus the player ERA divided by the league ERA and multiple by 100. In other words: 100 * (2 – playerERA/leagueERA).* That’s literally it. The advantage, of course, is that you can determine how much better than average a pitcher was, no matter what the run environment.
* They did change ERA+ just yesterday. It produces the same results, in that the players are ranked the same. The formula change just makes ERA+ linear. That is, a player with a 122 ERA+ is 22 percent better than league average. The old way didn’t handle it like this. Sean Forman, proprietor of Baseball Reference, explains: “With the new formula, the equation is linear, so if the league ERA is 4.50 and you have one pitcher at 3.50, one at 3.00 and one at 2.50 you get ERA+’s of 122, 133 and one at 144 (one is 22% better than the league, one is 33%, and one is 44% better). It seems to me the numbers make a little more sense this way.”
I’d like to see this expanded to FIP. It shouldn’t be hard to create FIP+, and I do wonder sometimes why it’s not a readily available stat. Probably because FIP stands fine by its own, since it’s not really based on the same value scale as ERA. Still, I do like the concept of adding context by scaling to 100. It gives us a one-glance idea of how a player performs compared to his peers.
Next up
There will be one or two more posts in this series, touching on some other offensive and pitching measures. The ones in the series so far, though, are the ones we’ll primarily use.